Image: Luis Diaz Devesa/ Moment/ Getty Images
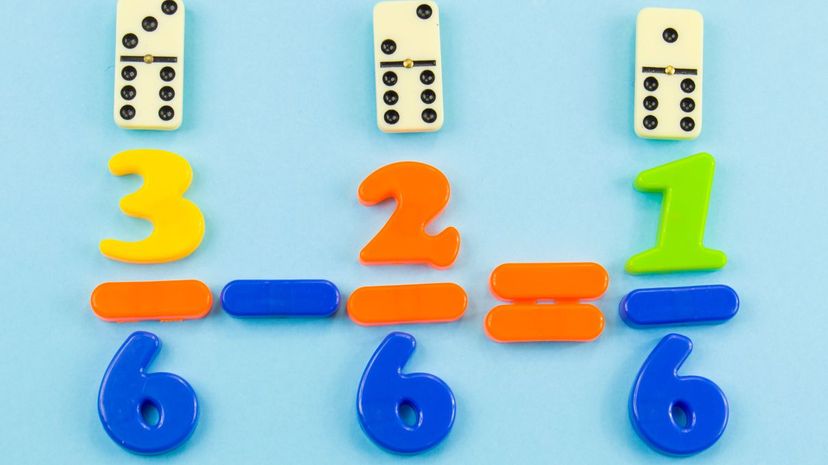
About This Quiz
When you were in school, did you love or hate math class? It seems to be one of those subjects that polarizes people. However, like it or not, you use fractions every day even without thinking about it. From dividing slices cake among friends to calculating your monthly budget, having at least a rudimentary understanding of fractions will make your life easier.
People have been learning about and using fractions for over 6,000 years. There's evidence that the Egyptians used fractions in their calculations around 4000 B.C. However, they had slightly different methods for solving problems and didn't use our current fraction notation. Greek mathematicians also used fractions before the year 0, but it wasn't until around 500 A.D. that fractions began to take their modern form. Mathematicians in India around this time wrote fractions as two numbers stacked on top of each other like modern fractions but without the bar between. The bar didn't come into use until around the year 1200, and the Moroccon mathematician Al-Hassar is credited as the inventor.
Can you remember how to add fractions properly? Does finding the lowest common denominator ring a bell? It's time to take a trip back to your middle school math class so grab your protector, ruler, and compass. Get started to see if you're a fraction genius!
4/5
9/10
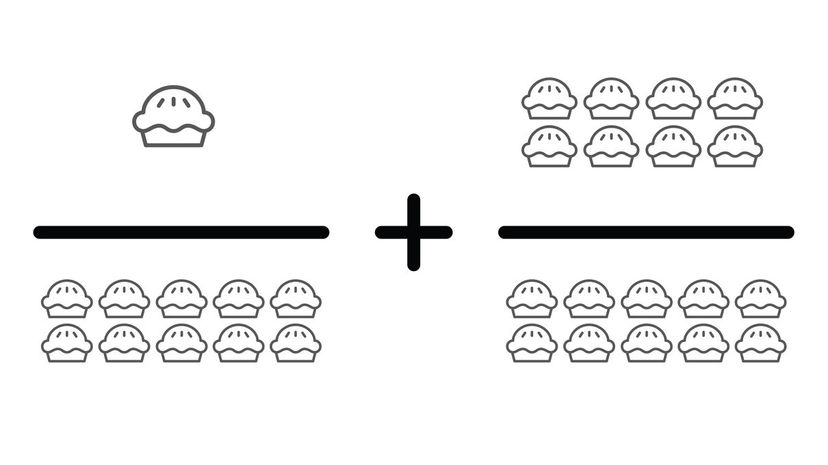
Do you have trouble with word problems? This problem is pretty straight forward (1/10+8/10). However, it can often be trickier having to read through a question and pick out the important information than solving the question by itself.
7/10
10/10
Advertisement
6
5 4/7
6 13/14
7 53/56
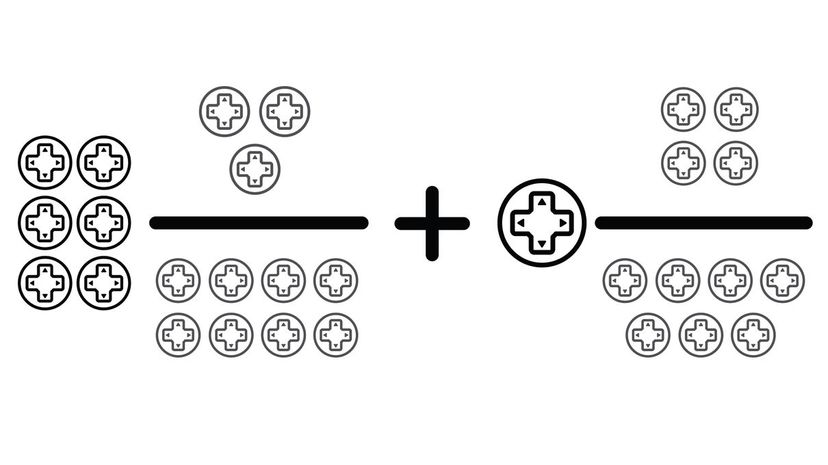
Remember, when we add mixed numbers, you can either convert each fraction back into an improper fraction or add the whole numbers together and add the fractions separately.
Advertisement
121/100
119/25
55/50
123/100
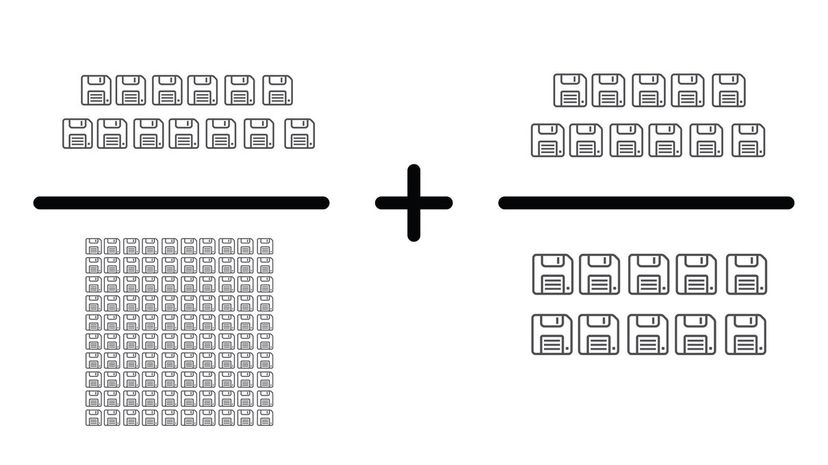
Are you starting to get the drill? Multiply the second fraction by ten to make its base 100 and then add the numerators together. You can right the answer as either 123/100 or 1 23/100 as a mixed fraction.
Advertisement
2 1/99
99/59
53/100
199/100
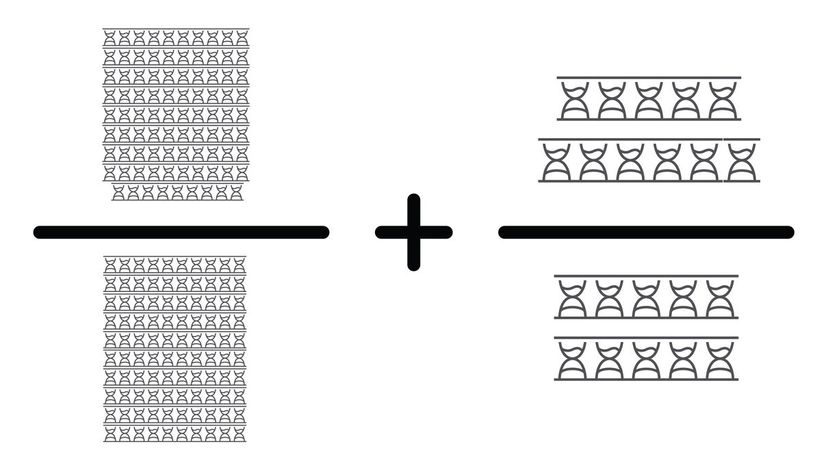
If you want to solve this problem, you'll have to multiply our second fraction by ten to make its base 100. From there, you can add the numerators to get 199/100 or 1 99/100.
Advertisement
-1/3
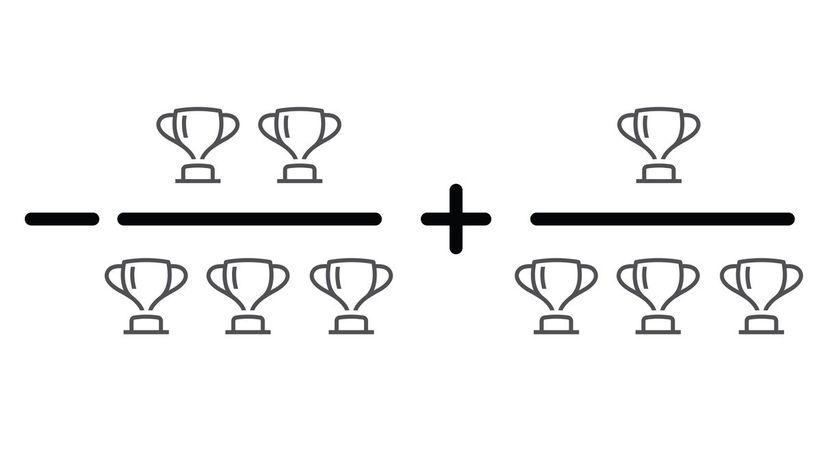
When you add negative fractions, you're essentially subtracting them from each other instead of adding. However, it's a little harder to conceptualize negative fractions with real-world examples. For example, if you have one-third of a cookie, it would be impossible for somebody to take two-thirds.
-1
1
1/3
Advertisement
11/20
9/20
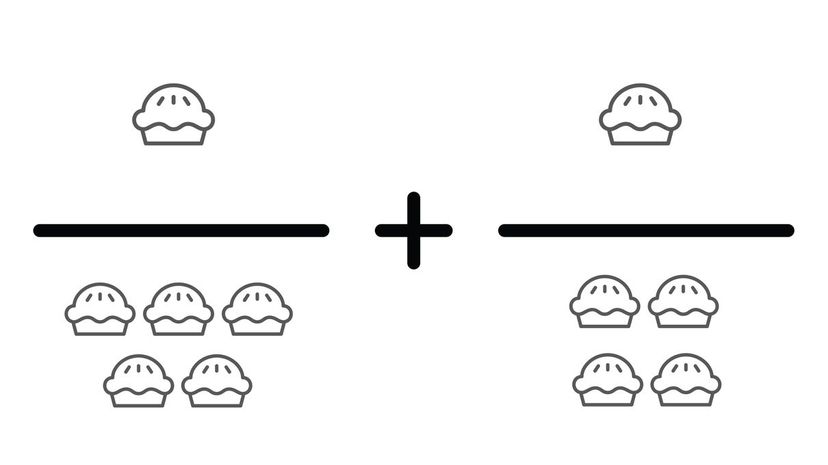
If you eat 1/5 of the pie the first time and 1/4 of the pie the second time, that's the equivalent of setting up the question as 1/4 + 1/5 = ?. Once we find a common base and add them together, we get 9/20.
1/2
1/3
Advertisement
3 5/12
3 2/3
4 1/3
5 1/12
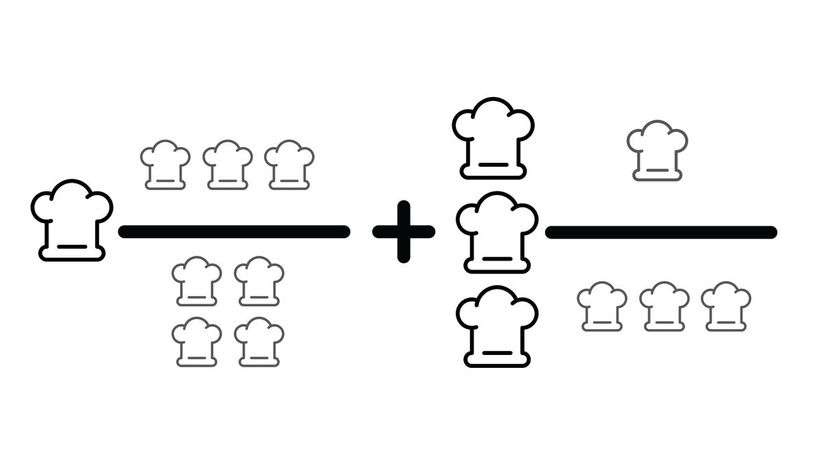
When solving this question, you can convert these fractions to 7/4 and 10/3. What's the lowest common denominator of four and three? Using base 12, we can convert these fractions to 21/12 and 40/12.
Advertisement
25/2
2 4/5
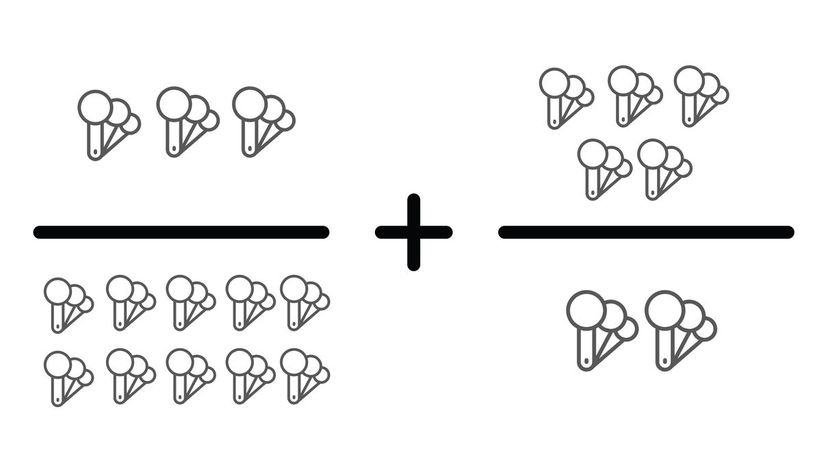
Since two is a multiple of 10, you can multiply our second fraction by five to get a common denominator. This turns our question in a summation of 3/10 + 25/10, which we can add together as 28/10 or 2 4/5.
4/5
19/10
Advertisement
2 1/200
2
1 197/200
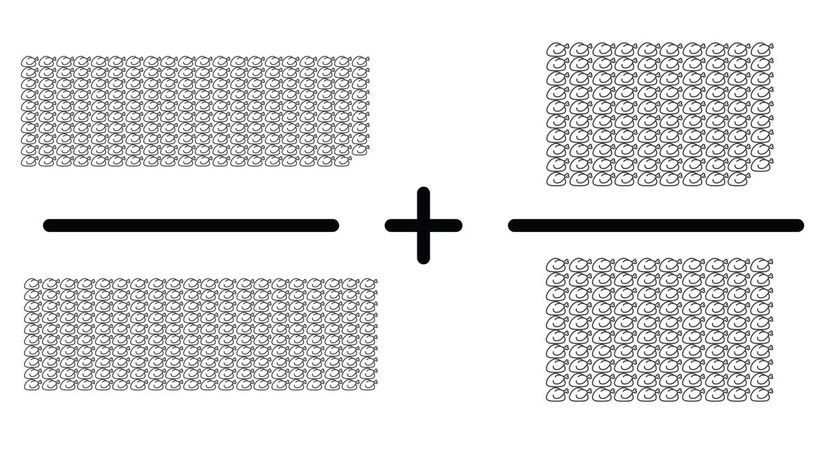
This summation requires one extra step from our last question. You need to double the second fraction to get a common base and then you can add 199/200 + 198/200 to get 397/200.
2 193/200
Advertisement
11/18
13/18
17/18
19/18
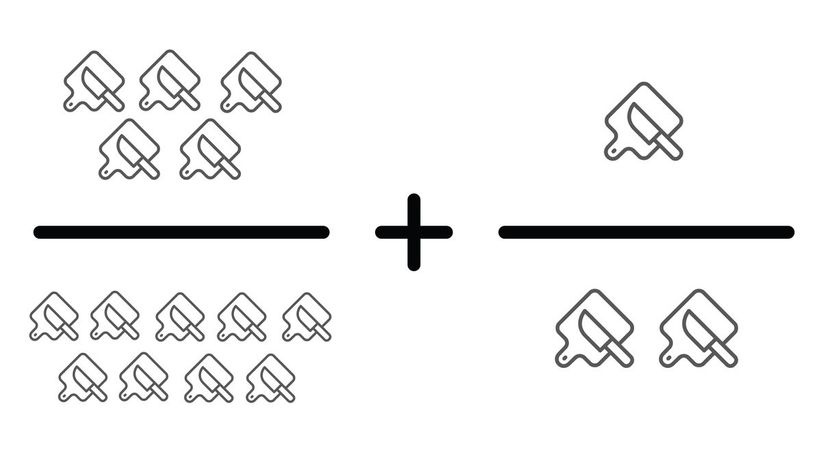
Can you spot the lowest common denominator that we can find with these two numbers? We can change this equation to 10/18+9/18. When we add them together, we get 19/18, which could also be written as 1 1/18.
Advertisement
1 1/2
2999/2000
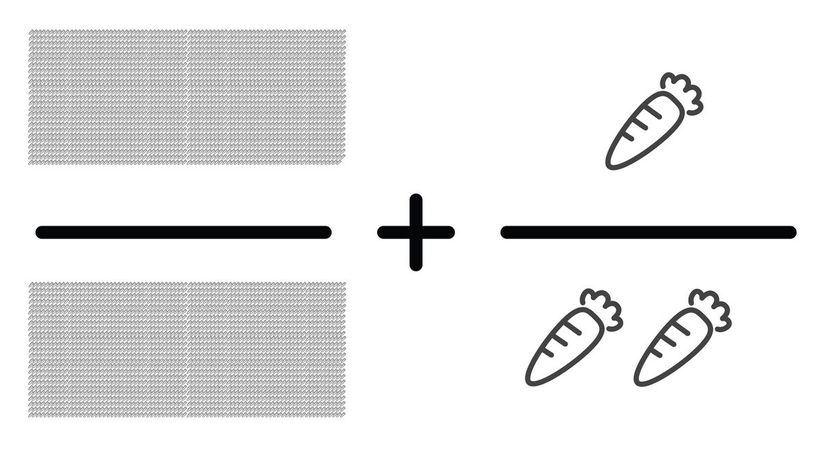
Even though it looks like there's a lot of work involved at a glance, you can just multiply the second fraction by 1000. 1999/2000 + 1000/2000 = 2999/2000. You could also write it as 1 999/2000.
2 1/2000
1999/2000
Advertisement
-1
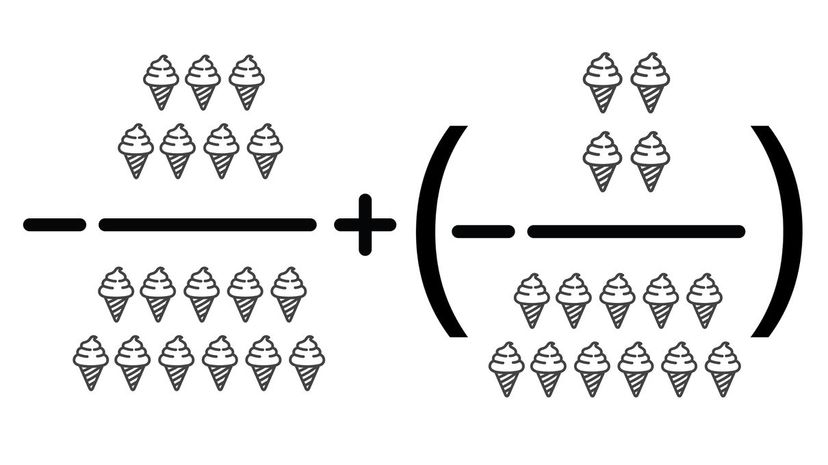
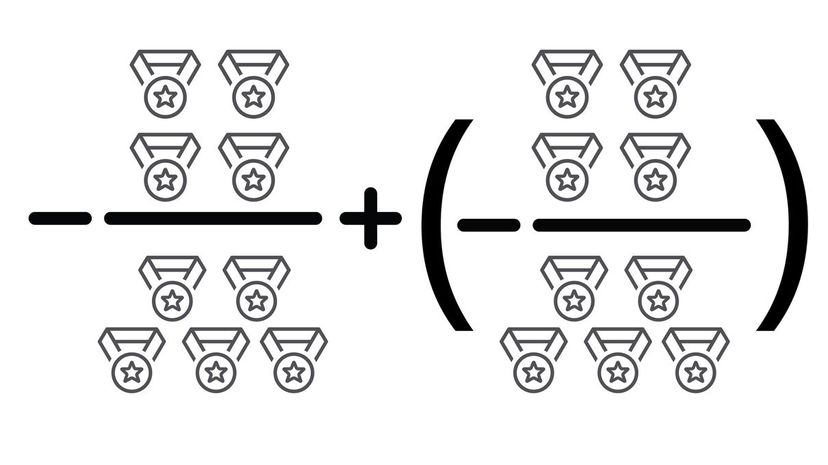
When you add -4/11, you're actually subtracting 4/11 from -7/11, giving a total of -11/11. You can reduce this to simply -1. Fractions with negatives aren't more difficult than regular fractions, but it can be tricky to keep track of the negative signs.
1
0
-10/11
Advertisement
15/24
1 3/10
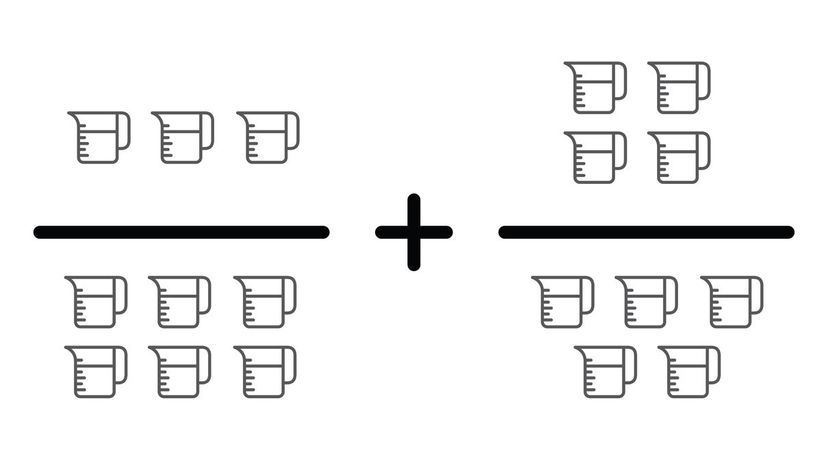
These two numbers share the common base of 30. When you add them together with a base of 30, you get 39/30. However, we can also turn this into the mixed number 1 9/30. Do you see a way to reduce this further? Since 9 and 30 are multiples of 30, we can condense to 1 3/10
3 1/10
37/30
Advertisement
14/10
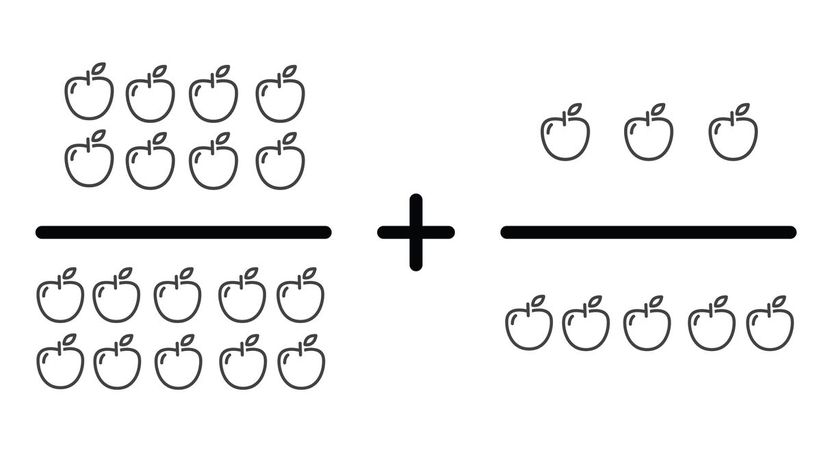
Remember, when you're adding fractions with different denominators (the bottom number), you have to make them the same before adding the two numbers. In this case, doubling 3/5 to make 6/10 gives us a common base.
12/10
11/5
12/5
Advertisement
-8/5
Both fractions are negative, so when you add them, you have to subtract a negative from a negative. You can solve the equation the same as an equation with positive fractions but by switching the sign.
0
1 3/5
-1
Advertisement
6/5
5/6
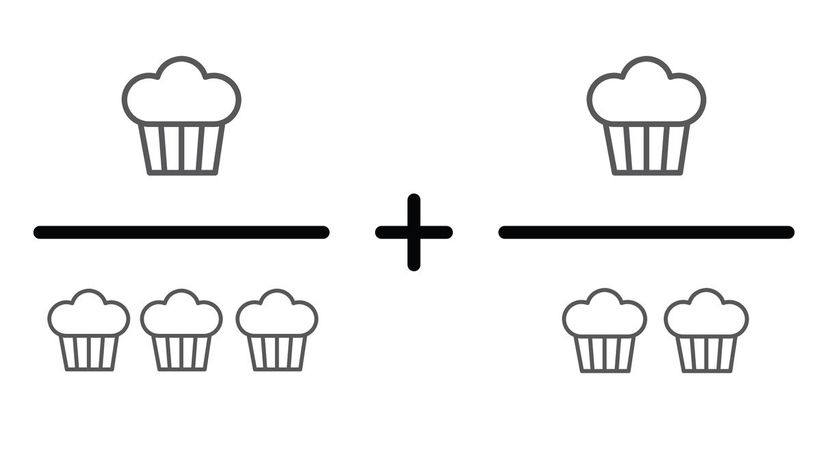
In order to get a common base for this question, you need to multiply 1/3 by two and 1/2 by three. That gives us the equation 3/6+2/6, which is much easier to solve now that we have a common base.
2/3
4/6
Advertisement
1/2
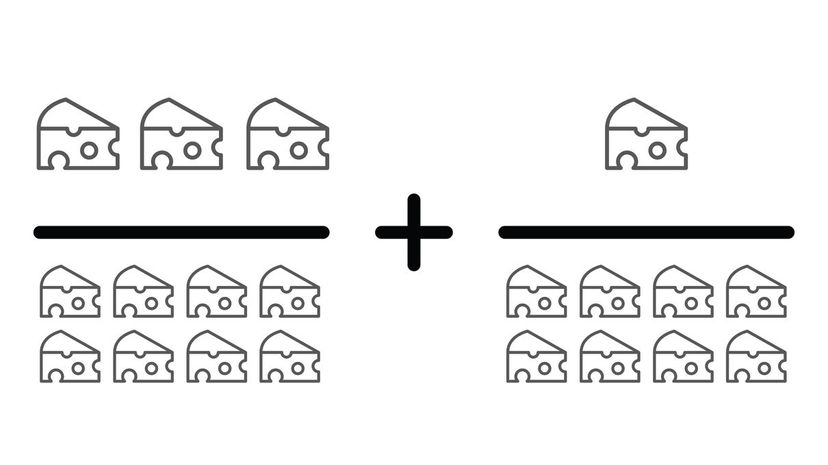
Summing these two fractions should be pretty straightforward. 1/8 and 3/8 share a common base so you can add the (numerators together). This gives you 4/8, which can reduce further to 1/2.
3/8
3/4
1/8
Advertisement
0
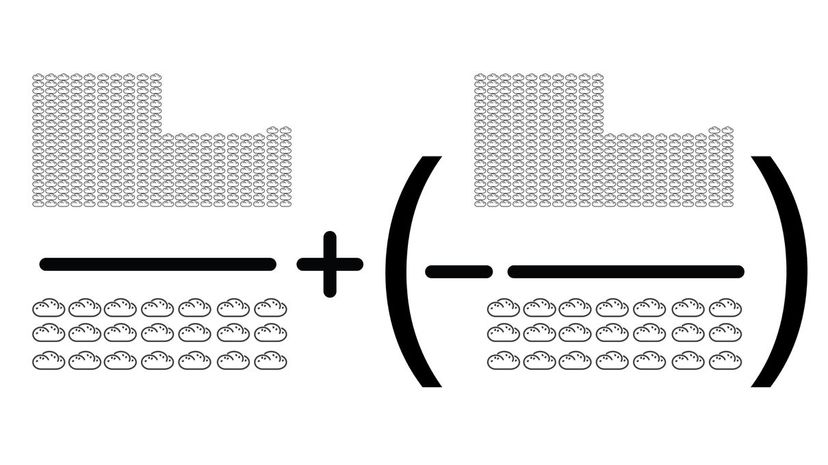
Remember, adding a negative fraction is the same as subtraction. When you subtract 312 from 312, you get 0. So 0/21 can be simplified to 0. Make sure you always check for negatives and double negatives!
312
21
614/21
Advertisement
11/126
125/126
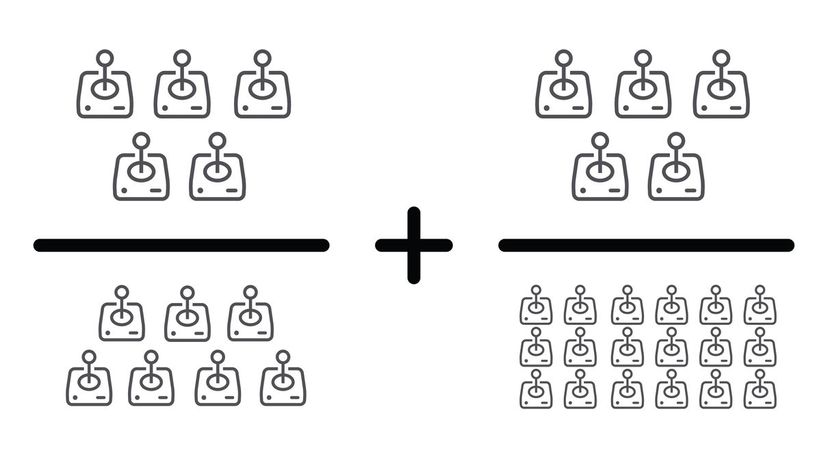
Even though the numerators are the same, you can't add fractions without making sure the denominators are also the same. The lowest common denominator of these two fractions is 126.
123/126
5 3/7
Advertisement
149/12
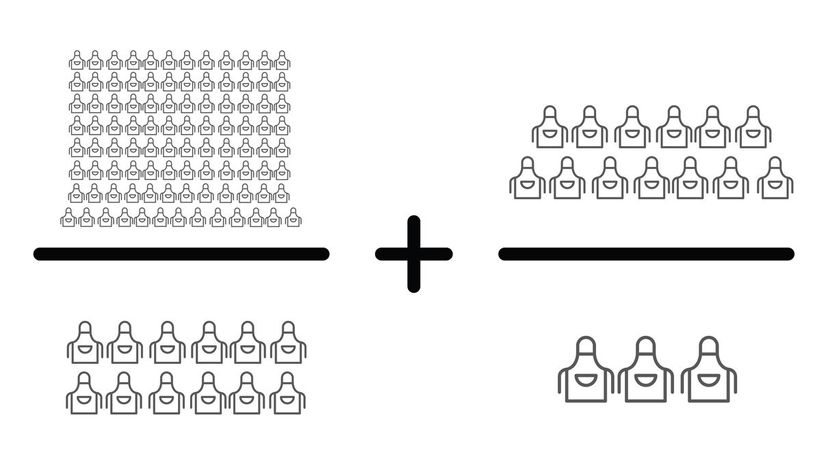
To find a common base for these two fractions, we don't have to look too hard. Since three is a multiple of four, we can multiply our section fraction by four to get 52/12. Then we can add our two fractions directly.
137/12
10 5/12
7 2/3
Advertisement
13 1/15
11 12/15
15 13/15
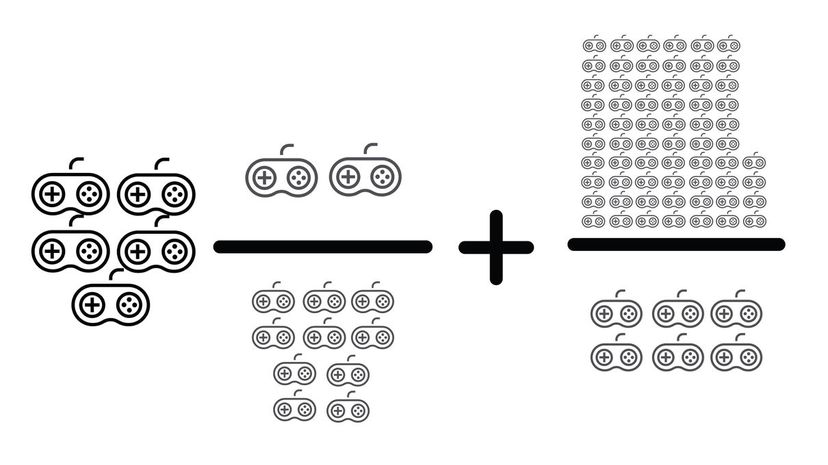
The way we recommend solving this question is by converting the first fraction to an improper fraction and finding a common denominator. The lowest common denominator in this question would be 30, which reduces to 15.
14 12/15
Advertisement
2 2/3
1 3/2
3 2/3
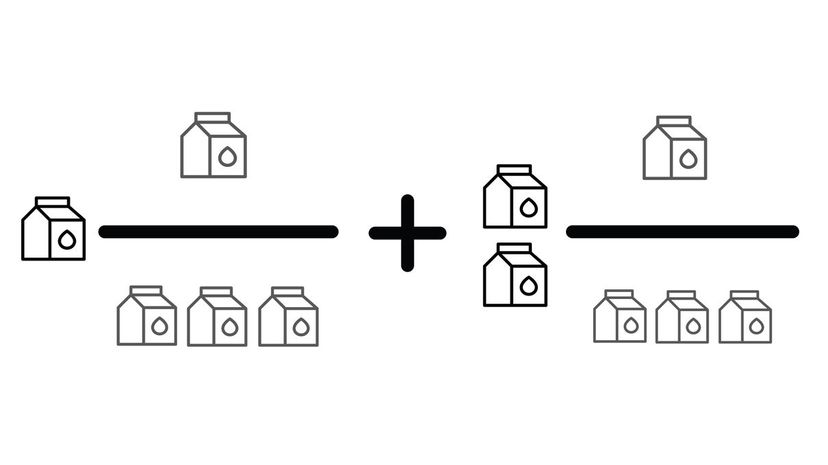
When you add mixed numbers together, you can add the full numbers together and then add the fractions separately. You can also convert the numbers back into improper fractions and add them together that way.
2 1/3
Advertisement
39/7
35/7
35/14
39/14
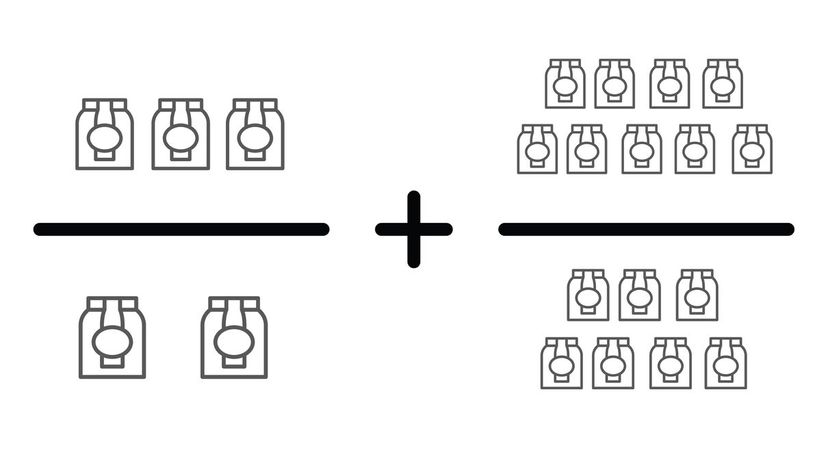
What's the lowest common denominator of these two fractions? Once we turn them in 21/14 and 18/14, we can add them together to get 39/14. What else can this be written as? You'd be correct if you said 2 11/14.
Advertisement
1 79/253
1 72/253
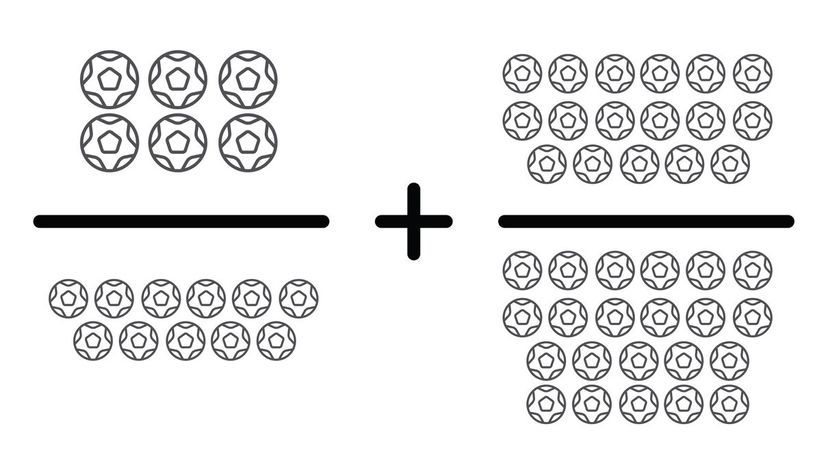
This equation follows the same pattern as our other questions, only it uses large numbers in the denominators. Multiply the first fraction by 23 and the second fraction by 11 to add the numerators.
1 1/3
1
Advertisement
53/114
113/114
32/114
67/114
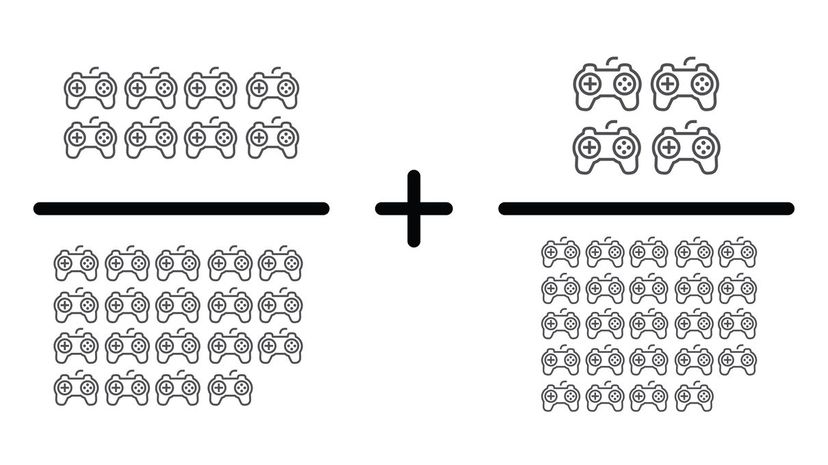
The hardest part of this question is dealing with the large numbers that come from finding a common denominator. If you multiply 19 by 24 to get a common base, you end up with 192/456 + 76/456.
Advertisement
183/14
-17/14
-183/14
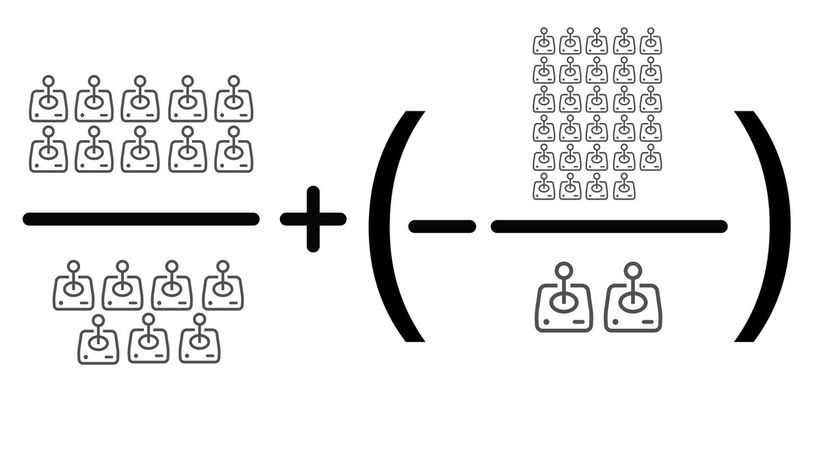
Our first fraction is positive while the second fraction is negative, which means we're going to end up with a negative number. Once we find the lowest common denominator, the question becomes 20/14 - 203/14.
12 3/14
Advertisement
7 1/12
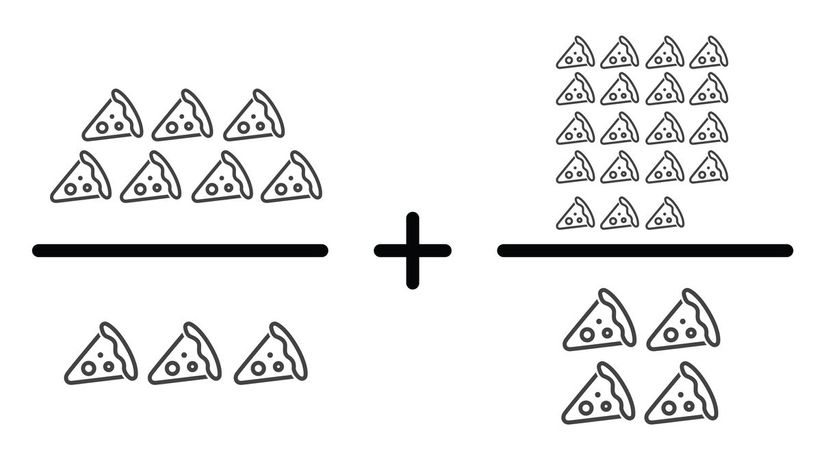
Hopefully, you understand how we came to this answer. When you multiply the two fractions to find a common denominator, you get 28/12 + 57/12, which gives a sum of 85/12.
8 11/12
6 11/12
5 5/6
Advertisement
221/30
7/30
229/30
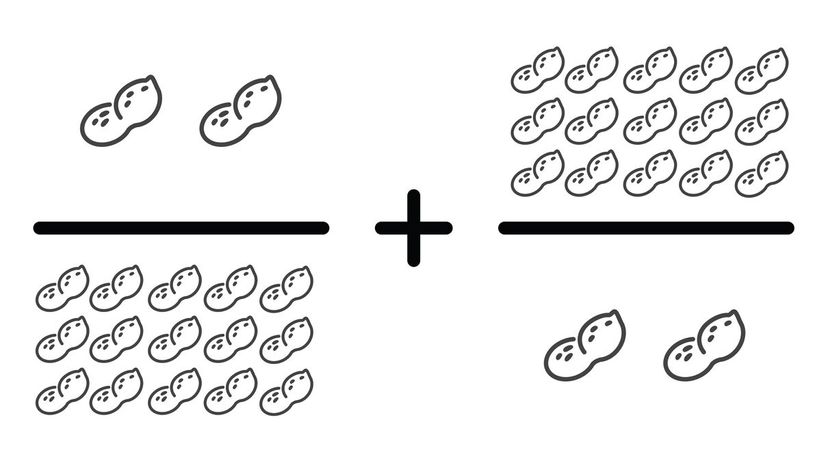
Wouldn't it be nice if you could add these two fractions together to make 17/17? That would solve a lot of trouble, but unfortunately, you have to find a common denominator and go through our usual steps.
30/7
Advertisement
203/104
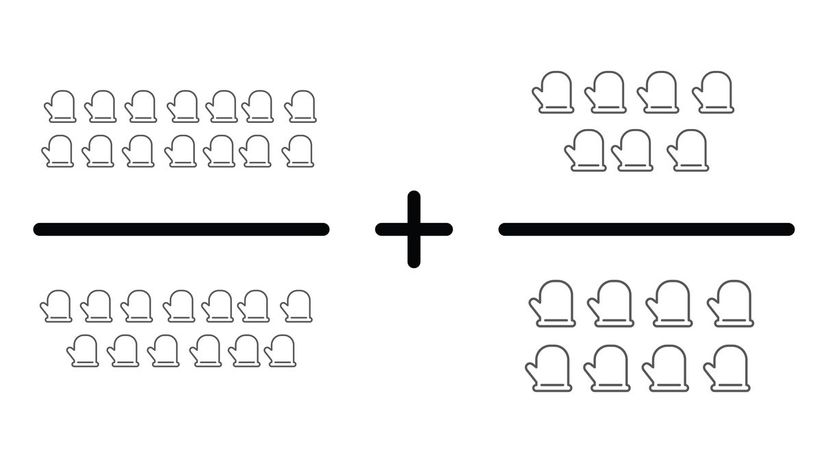
Unfortunately, the lowest common denominator of these two numbers is 104, which means you'll have to o a lot of multiplication before adding these two fractions together. These fractions add to 203/104 or 1 99/104.
197/13
212/8
193/104
Advertisement
69/114
77/114
67/114
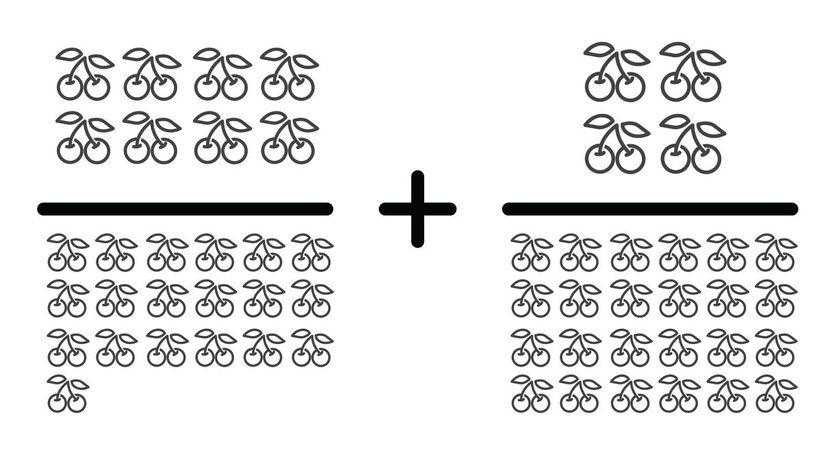
Have you learned the pattern by now? You can multiply 19 by 24 to find a common denominator and add the numerators together. After reducing the fractions to a base of 114, you get 67/114.
12/19
Advertisement
33/35
37/31
31/37
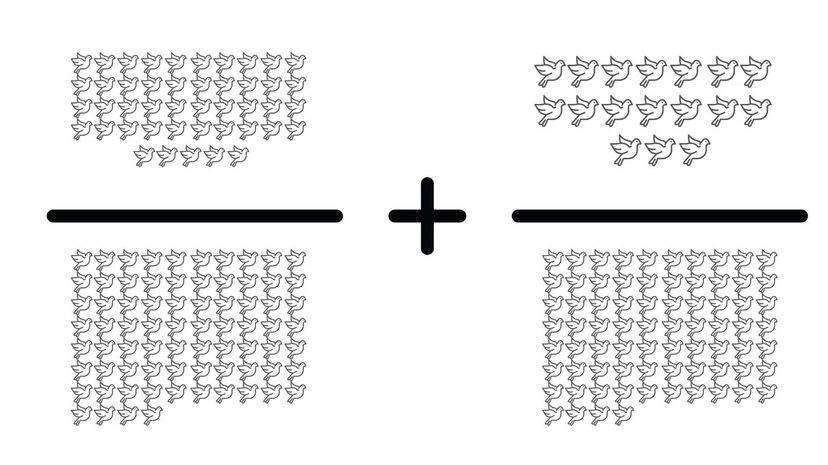
Originally 45/74 pigeons flock toward you. After the second handful of breadcrumbs, 17/74 pigeons flock toward you, which sums to 62/74 pigeons in total. This can be reduced to 31/37.
19/74
Advertisement
26/35
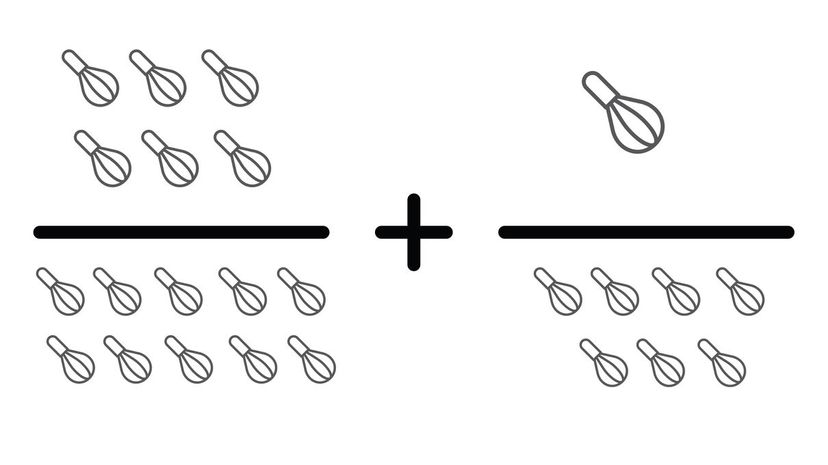
You can use the same steps to solve this problem as our first few questions. Since our numbers have different bases, you need to find a base they have in common. In this case, that base is 70, which can be reduced to 35 after the addition.
5/9
31/35
29/70
Advertisement
1 187/188
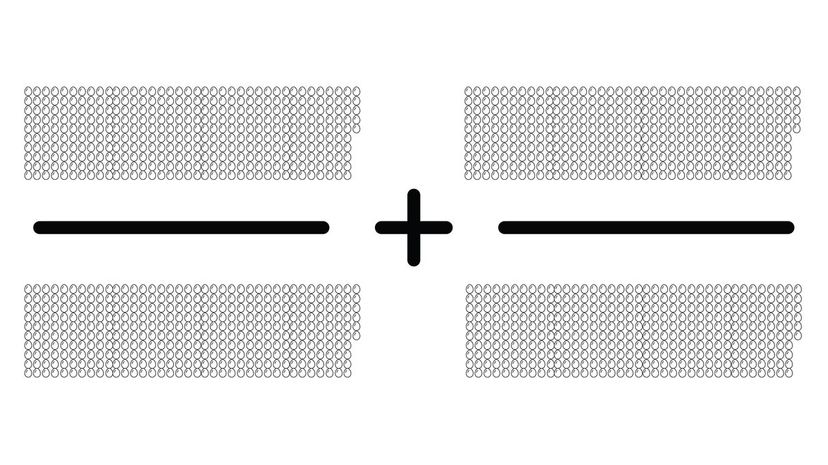
Actually, this question isn't much harder than the others even though we used higher numbers! Since the bases are already the same, you can add the numerators together normally.
1 375/376
2 1/376
1 185/188
Advertisement
19/26
1/3
10/13
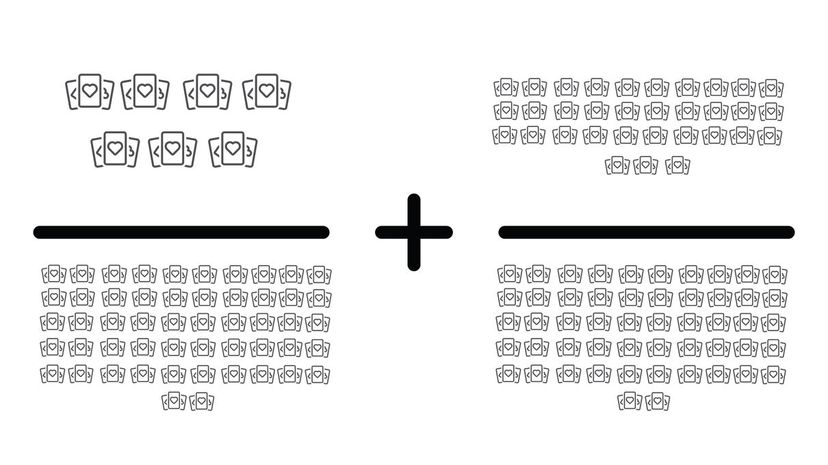
The key to this question is to be able to pick up the vital information in the question and to be able to reduce the fraction. Since you picked up 7/52 and 33/52 cards, you picked up 40/52 cards in total, which can be reduced to 10/52.
1/4
Advertisement
2 1/2
3
2 453/2000
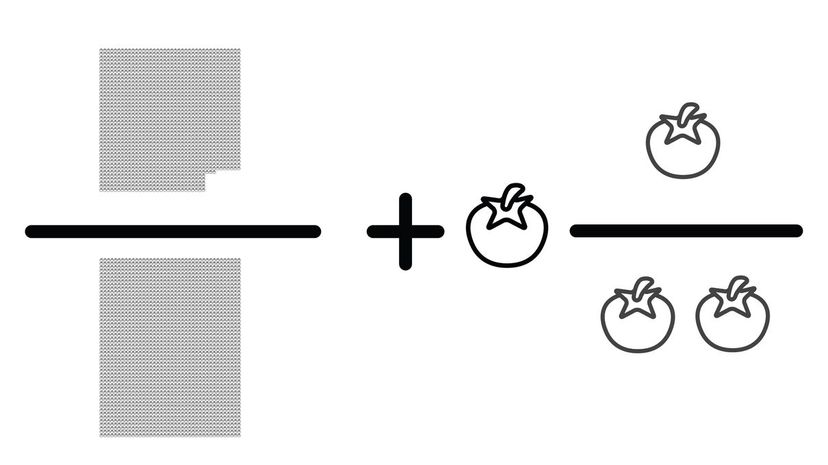
There are several ways to solve this question, but perhaps the easiest is to convert the second number into a mixed number and multiply by 1000 to get 1543/2000 + 3000/2000 = 4543 /2000
2 1/2000
Advertisement
You Got:
/35
